什么是傅立叶变换
关于傅立叶变换,可以用果汁牛奶打一个比方:
- 什么是傅立叶变换:对于一杯果汁牛奶,能分析出其食谱(recipe)
- 如何进行傅立叶变换:运行果汁牛奶的过滤器(filters),将各类成分(ingredient)分离(extract)出来
- 为什么要进行傅立叶变换:食谱要比果汁牛奶要容易分析、比较、修改得多
- 如何再变换回去:根据食谱将成分再混合到一起,就又得到果汁牛奶了
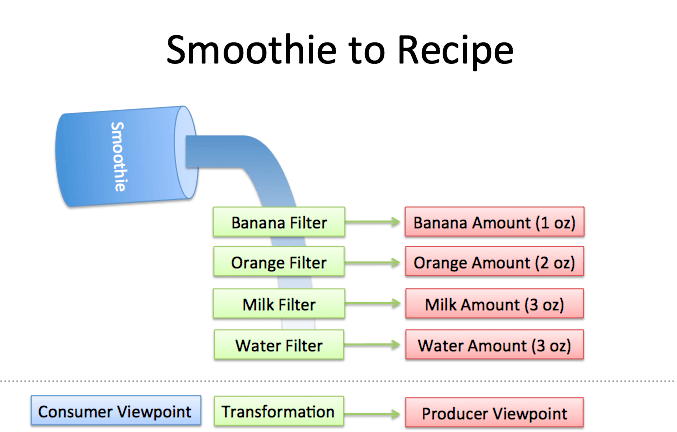
总之,对果汁牛奶进行傅立叶变换后,我们的视角(perspective)从消费者变成了生产者,从 “What did i see” 变成了 “How was it made”,Recipe 比 Object 本身更容易进行分析、比较、修改。
所谓“变换”,就是换个领域看问题(A Change Of Perspective),将某种情况下不易分析处理的领域换成易分析处理的领域
好,让我们看看真正的傅立叶变换,维基百科上的一张GIF图清晰明了,可以看出:
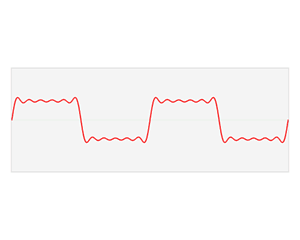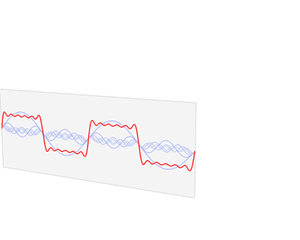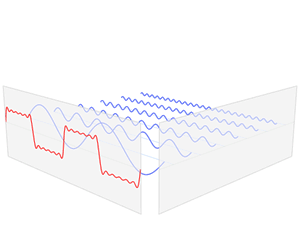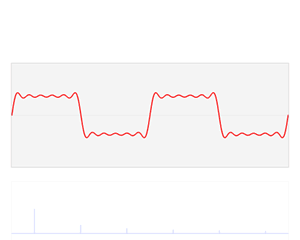
- 任何连续周期信号都可以由一组适当的正弦曲线组合而成(这些正弦曲线通过叠加逼近,直至误差可以忽略)
- 连续周期信号的表象是时域(time domain)波形,从时域上,我们很难进行分析、处理,因此我们需要从另外一个维度去分析信号,而傅立叶变换就是将信号从时域(Observations In The Time Domain)转换到频域(Ingredients In The Frequency Domain)。为什么要到频域呢?频率只是信号的一个特征,但是它可以用来识别信号,在频域可以得到信号的成分(ingredients),就像果汁牛奶一样,Recipe 比 Object 本身更容易分析、比较、修改
分离信号与傅立叶变换的应用
从上面可以看出,傅立叶变换说到底就是分离信号,可为什么要分离信号呢?其实信号只是信息的载体,信息无处不在且多种多样,因此信号的类型也多种多样,但是在传输的方式却比较少(每一种的容量非常大),例如声音、光线、电磁等等。由于同一种传输方式的容量非常大,将信道分成不同区域同时使用,信道的利用率大大的提高了。
但是问题来了:虽然对信道进行划分,但是信号在相同的信道中传输时,大自然不管你如何划分,都是按同样的方式传输,不同类型的信号被合在一起进行传输,就像上面的果汁牛奶,不管你把各类成分划分得如何清晰,果汁机出来就是混合过的果汁。这时,接受端就需要对信号进行分离,识别出不同的信号,进行分析处理。分离信号是我们最常见的事情,我们无时无刻不在进行,以至于根本没有注意到。例如,看到不同的颜色,尝到不同的味道,听到不同的声音(对于振动产生的声音,在传播时不管高低音,是缠在一起在介质中传输的,但是人耳可以分辨出)。
傅立叶变换只是分离信号方法中的一种(靠频率分离),由此可以想到傅立叶变换的一些应用有:
- 滤波:将不需要的频率对应的信号过滤掉,只留下需要的信号
- 调频:基于滤波,只专注于特定频率的信号进行接受
- 去噪:通过分离,把噪声对应频率的信号处理掉,增强核心的信号
- 压缩:将那些不太重要的部分忽略掉,保留主要部分(有损压缩)。例如,JPEG对.bmp压缩,MP3对.wav压缩都是这种方式
参考资料
我喜欢那种深入浅出,生动有趣的资料,而不是死板的公式与定理,所以下面的资料都非常有趣,看完能很快对傅立叶变换有初步的理解: